Design & Simulation

Design

The KIT-D structure was designed using caDNAno, taking inspiration from the mechanism of an origami folding method called Kresling folding. Kresling folding is a pattern of periodic concavo-convex folds that fold a piece of paper into a tube without cutting or adding parts. The basic mechanism of Kresling folding is similar to that of another folding method called Miura folding in which a paper is folded with periodical concavo-convex folds. We referenced the basic design of Miura folding made with DNA origami by the 2018 Team Sendai project [1].

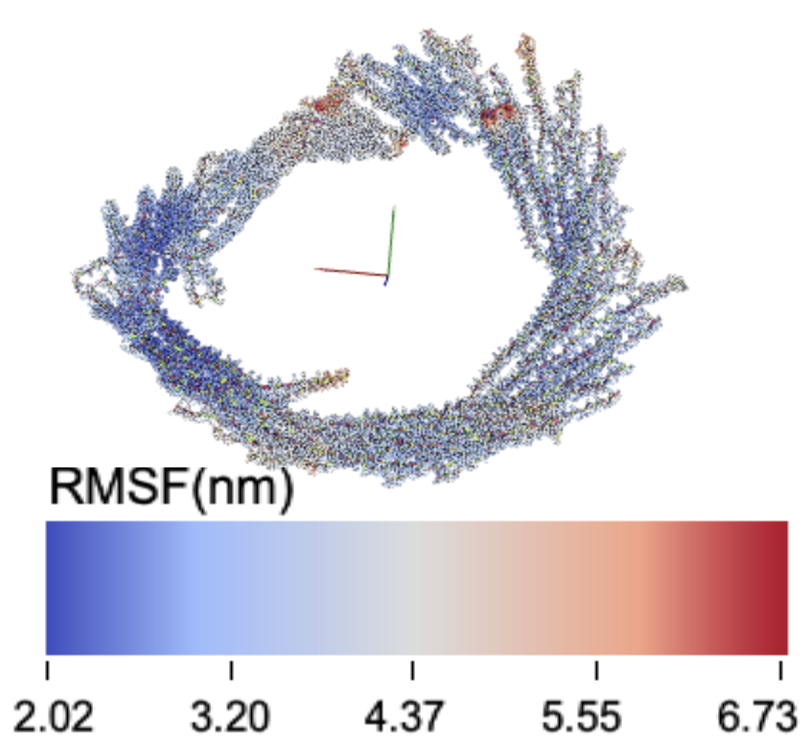
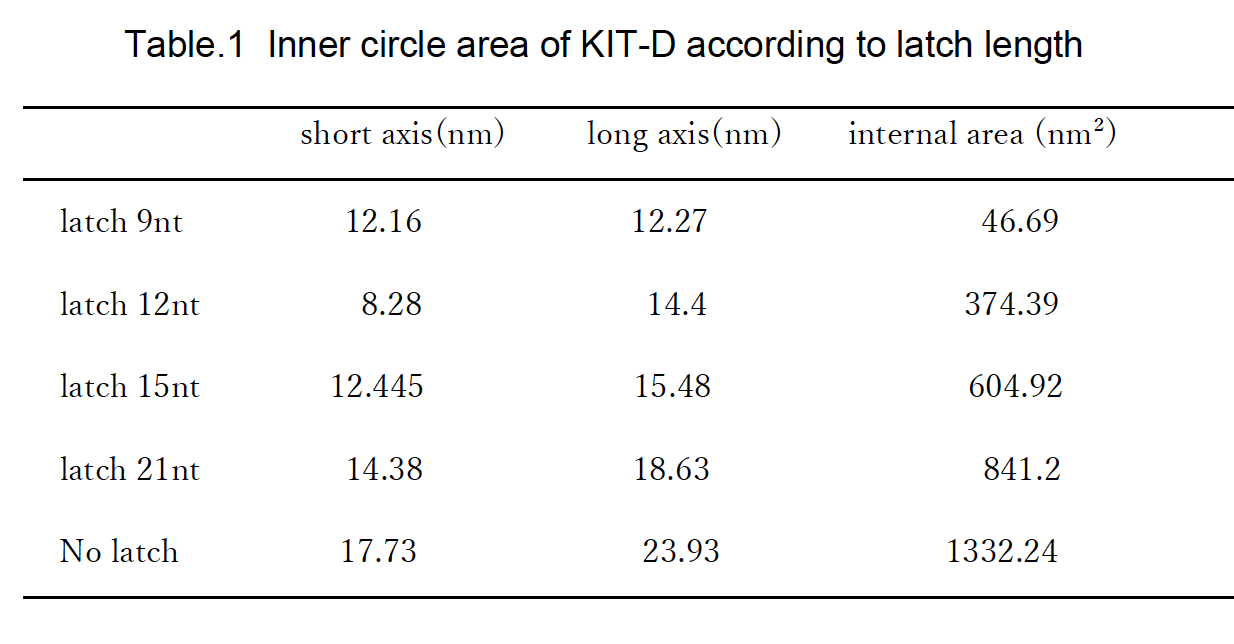
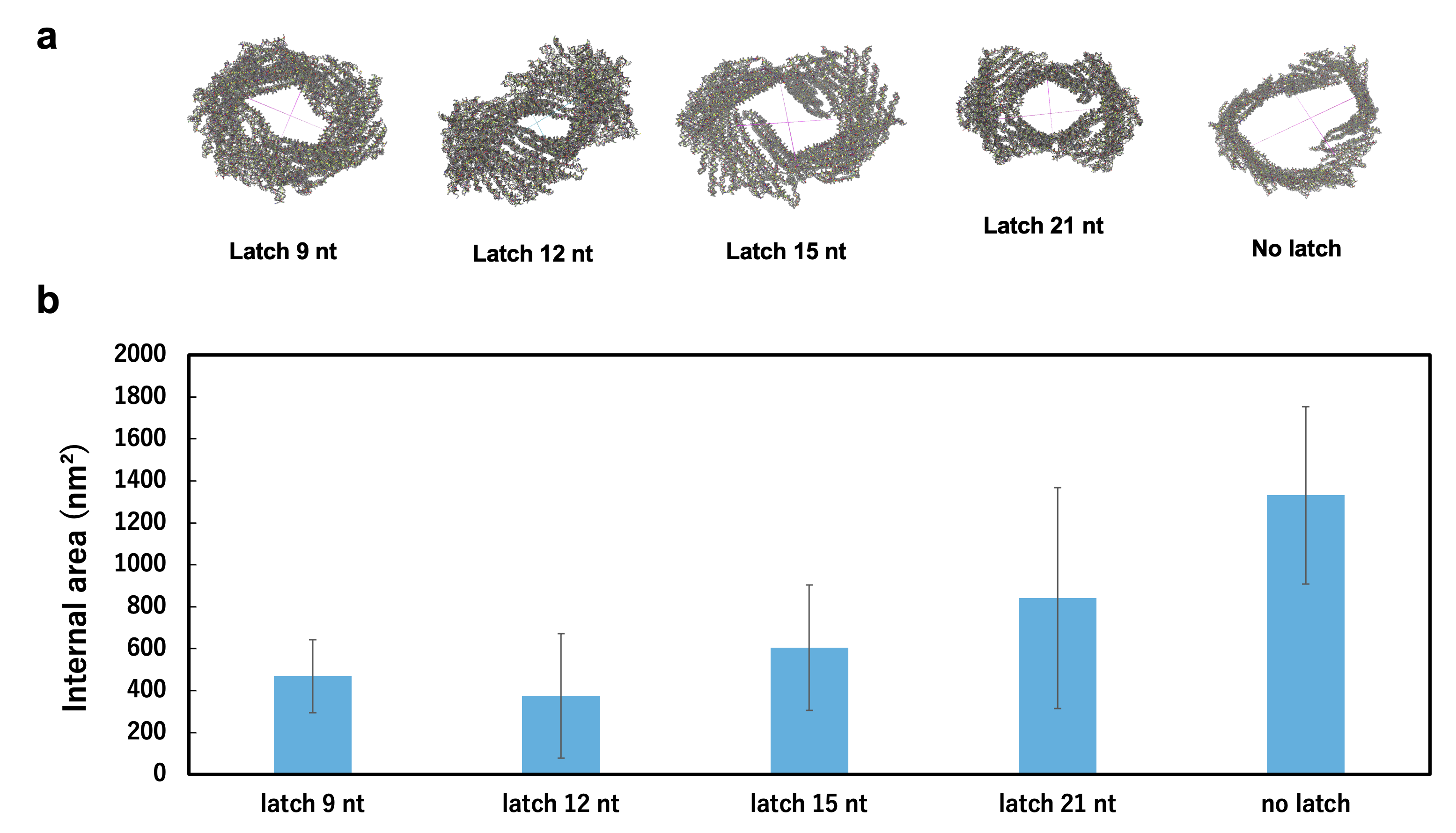
Determining the aspect of the structure

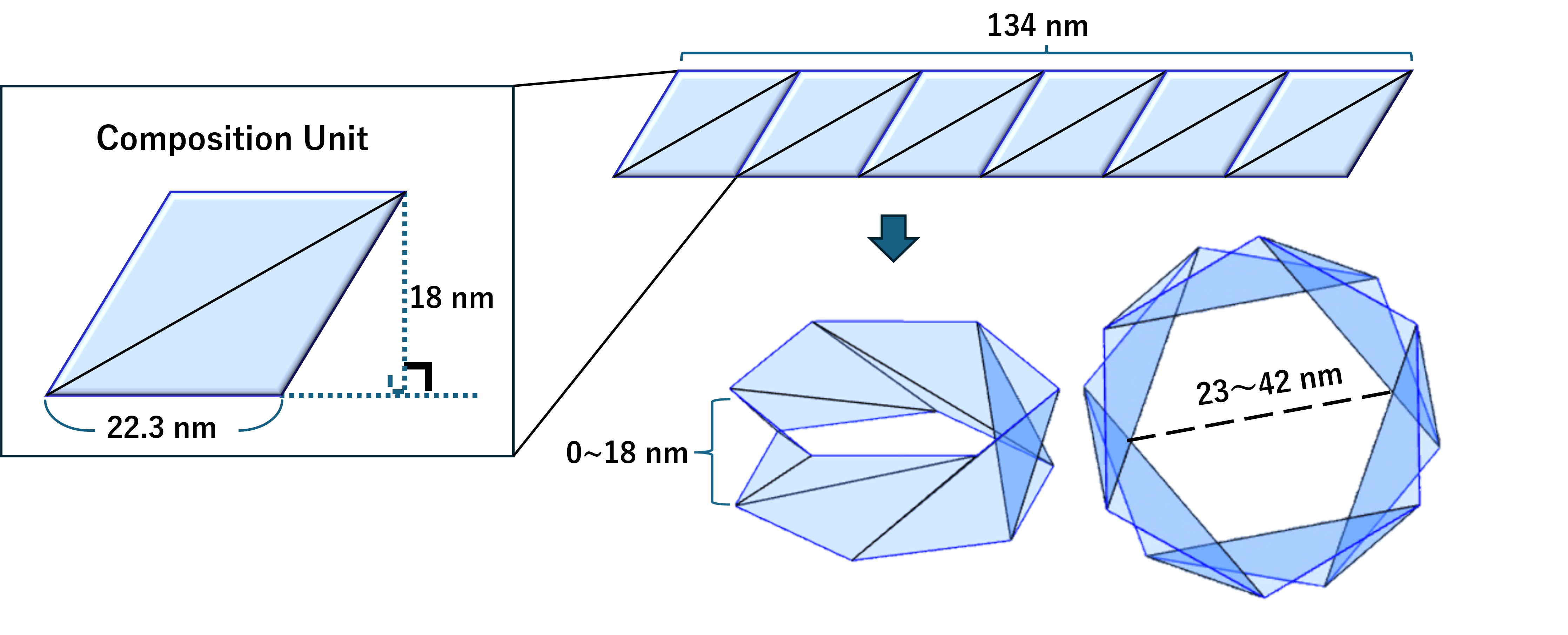
The major advantage of Kresling folding is its ability to adjust the tube length and inner diameter. In Kresling folding, the addition of faces creates additional creases, making the folding process easier, while fewer faces increase folding difficulty. Using paper models, we sought for a shape that requires enough rigidity for transformation while having enough flexibility to fold in, resulting in the outer circumference to be designed as a regular hexagon (figure 1). This hexagonal shape also has the benefit of retaining enough area of both the structure and the inner hole when in the closed form, making it easier to recognize the structure when observing.

Figure 1. The basic dimensions of KIT-D

This figure shows the dimensions of the KIT-D structure. It is made of a series of six parallelograms composed of two isoceles triangles which are placed back to back. The parallelogram unit can be rolled up into a tubular structure with height ranging from nearly 0 to 18 nm, and its inner diameter changing from 23 to 42 nm.

The core framework of KIT-D was constructed by arranging a series of parallelograms composed of two opposing triangles. A unique aspect of Kresling folding is that the angle of each small triangle and the angle that the parallelogram composes with the base impact key structural characteristics. Specifically, the smaller triangular angle, shown as α in figure 2, also dictates the shape of the outer perimeter. For example, an isosceles triangle with α as 60° yields a regular triangle for its perimeter. For α with an angle of n°, the outer perimeter will form a polygon with 180/n number of sides. Additionally, the pore size of the tube is influenced by the external angle at the parallelogram’s base, which is represented as β in Figure 2.

Figure 2. Angles of parallelogram related to structure formation

The angle shown in α here is known to determine the shape of the outer perimeter, in which the outer perimeter forms a polygon with 180/n number of sides, if α is n degrees. The angle shown as β affects the size of the pore of the Kresling tube.

Two-layered structure to enhance rigidity

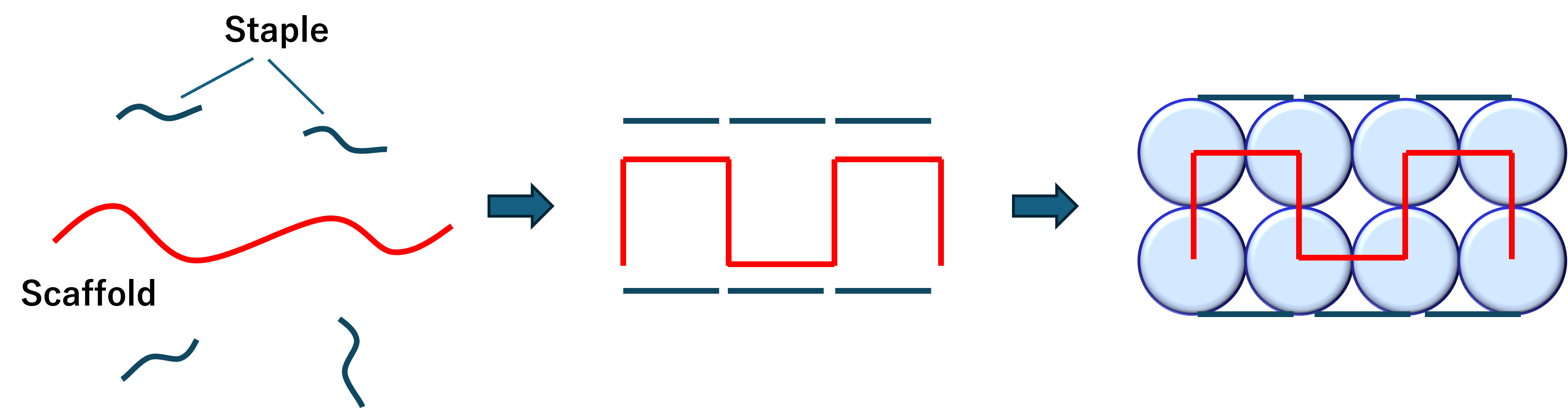
To reinforce structural rigidity, KIT-D employs a dual-layered configuration. This two-layer is designed to enhance durability compared to a single-layered structure. Each structural face has a two-DNA-layer thickness, corresponding to about 4 nanometers. This was achieved by meandering the scaffold DNA and securing it with staple strands. The bilayer configuration also introduces a distinction between the top and bottom of each face, facilitating controlled hinge and latch mechanisms, which will be elaborated upon below.

Figure 3. Formation of the two-layered structure

Staple strands were designed to fix the scaffold strand in a meandering way to form two layers, providing durability to the structure.

Adjusting the length and position of the hinges

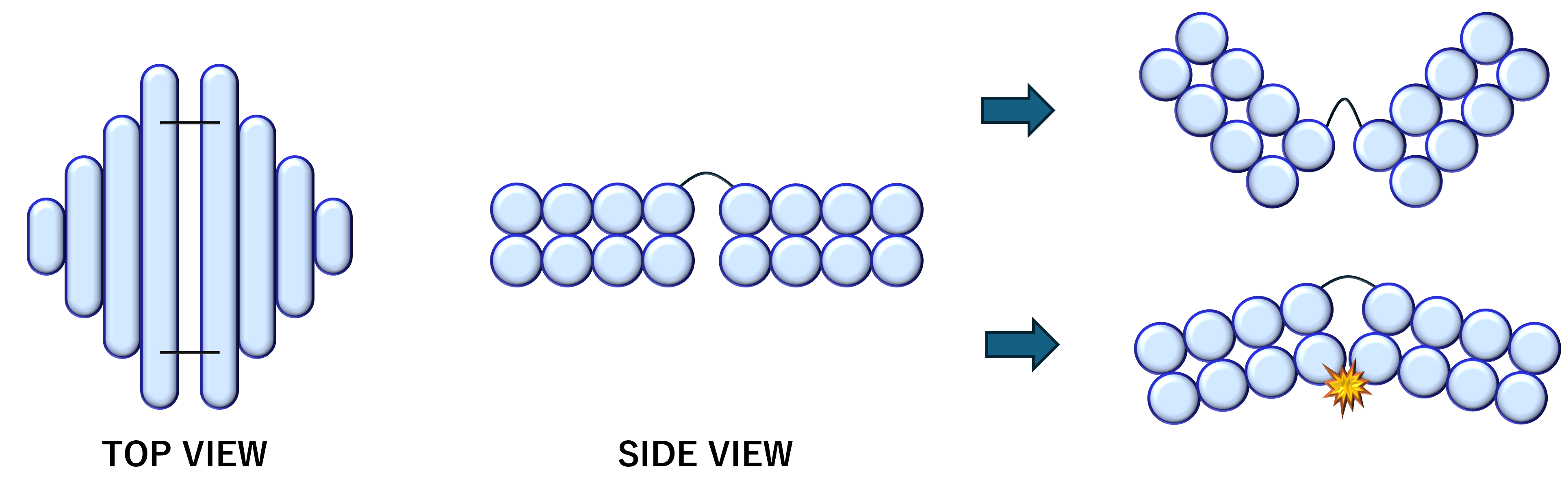
To optimize the structural mobility, careful adjustments were made to the length and placement of hinges, which introduce flexibility and enable precise angular adjustments at targeted structural sites. Each hinge, with a length of 3 nucleotides, attaches to only one of these two layers, creating an asymmetry that directs the folding in a specific orientation (figure 4). This configuration facilitates easier folding in the intended direction while preserving rigidity in the opposite direction. This mechanism enables the adaptation of mountain folds and valley folds in desired locations that are required for the Kresling folding.

Figure 4. Positioning of the hinges to guide folding direction

Hinges were located on one side of the layer to navigate the direction of the folding, enabling the implementation of mountain and valley folds in desired positions.

Structural Design for Transformation

A latch mechanism was integrated to stabilize the closed structure. Each triangular unit features a latch attached to the tips of two opposing, inverted triangles (figure 5a). In their default state, these latches exist as free single strands, each anchored at one end. In the open state, each face of the structure waver and randomly takes different forms. When a complementary single strand, referred to as “close,” is introduced, it hybridizes with both latches when the top and bottom triangles are close to each other during the random transformation, fixing the structure in a closed state (figure 5b). To enable controlled detachment, an additional strand, “anti-close,” can be introduced. Anti-close strand is fully complementary to close, allowing it to hybridize and displace close strand from the latches, effectively releasing the structure back to its open state (figure 5c). Various latch lengths were tested to optimize the balance between structural stability and the visibility of the deformation process.

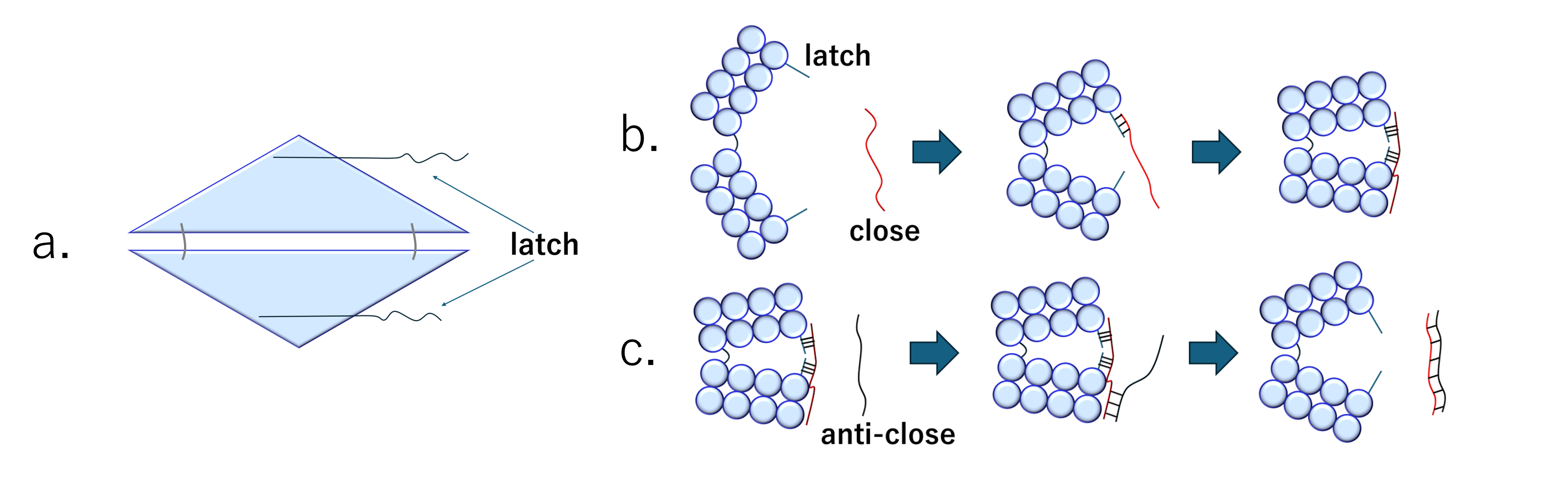
Figure 5. Positioning of latches and transforming mechanism

5a. shows that the latches are located at the tips of the triangles.
5b. illustrates how KIT-D closes when an additional strand “close” is added.
5c. shows the transformation of the structure to its open state when ”anti-close” is added.